Next:

An atom is the smallest unit of ordinary matter that forms a chemical element. Every solid, liquid, gas, and plasma is composed of neutral or ionized atoms. Atoms are extremely small, typically around 100 picometers across. Gen atom, the order of increasing orbital energy is given by 1s helium. Similarly, 3s, 3p and 3d increase energy in that order, and so on.

Hydrogen Molecule Ion Up:Variational Methods Previous:Variational Principle
A helium atom consists of a nucleus of charge surroundedby two electrons. Let us attempt to calculate its ground-state energy.

Let the nucleus lie at the origin of our coordinatesystem, and let the position vectors of the two electrons be and , respectively. The Hamiltonian of the system thustakes the form

where we have neglected any reduced mass effects.The terms in the above expression represent the kinetic energy of the firstelectron, the kinetic energy of the second electron, the electrostaticattraction between the nucleus and the first electron, the electrostaticattraction between the nucleus and the second electron, and theelectrostatic repulsion between the two electrons, respectively.It is the final term which causes all of the difficulties. Indeed, if thisterm is neglected then we can write

(1181)

where
In other words, the Hamiltonian just becomes the sum of separate Hamiltonians for each electron. In this case, we would expect thewavefunction to be separable: i.e.,

(1183)

Hence, Schrödinger's equation
reduces to

(1185)

where
Of course, Eq. (1185) is the Schrödinger equation of a hydrogen atom whosenuclear charge is , instead of . It follows, from Sect. 9.4 (making the substitution ), that if both electrons are in their lowest energystates then

(1187)

(1188)

where

He Atom Size

Here, is the Bohr radius [see Eq. (679)]. Note that is properly normalized. Furthermore,

(1190)

where is the hydrogen ground-stateenergy [see Eq. (678)]. Thus, our crude estimatefor the ground-state energy of helium becomes
Unfortunately, this estimate is significantly different from the experimentallydetermined value, which is . This factdemonstrates that the neglected electron-electron repulsion term makes alarge contribution to the helium ground-state energy.Fortunately, however, we can use the variational principle to estimate this contribution.

Let us employ the separable wavefunction discussed above as our trialsolution. Thus,

(1192)

The expectation value of the Hamiltonian (1180) thus becomes
where

(1194)

The variation principle only guarantees that (1193) yields anupper bound on the ground-state energy. In reality, we hopethat it will give a reasonably accurate estimate of this energy.

It follows from Eqs. (678), (1192) and (1194) that

where . Neglecting the hats, for the sake of clarity, the aboveexpression can also be written

(1196)

where is the angle subtended between vectors and .If we perform the integral in space before that in space then
where

(1198)

Our first task is to evaluate the function . Let be a set of spherical polar coordinates in space whose axis of symmetry runs in the direction of . It followsthat . Hence,

which trivially reduces to

(1200)

Making the substitution , we can see that
Now,

(1202)

giving
But,

(1204)

(1205)

yielding

Since the function only depends on the magnitude of ,the integral (1197) reduces to

(1207)

which yields
Hence, from (1193), our estimate for the ground-stateenergy of helium is

(1209)

This is remarkably close to the correct result.

We can actually refine our estimate further. The trial wavefunction (1192) essentially treats the two electrons as non-interacting particles. Inreality, we would expect one electron to partially shield the nuclearcharge from the other, and vice versa. Hence, a bettertrial wavefunction might be

where is effective nuclear charge number seen by eachelectron. Let us recalculate the ground-state energy of heliumas a function of , using the above trial wavefunction, and thenminimize the result with respect to . According tothe variational principle, this should give us an even better estimatefor the ground-state energy.

We can rewrite the expression (1180) for the Hamiltonianof the helium atom in the form

(1211)

where
is the Hamiltonian of a hydrogen atom with nuclear charge ,

(1213)

is the electron-electron repulsion term, and
It follows that

(1215)

where is the ground-state energy of a hydrogenatom with nuclear charge , is the value of the electron-electron repulsion term whenrecalculated with the wavefunction (1210) [actually, all weneed to do is to make the substitution ], and
Here, is the expectation value of calculatedfor a hydrogen atom with nuclear charge . It follows fromEq. (695) [with , and making the substitution ] that

(1217)

Hence,
since . Collecting the various terms, our new expression for the expectationvalue of the Hamiltonian becomes

(1219)

The value of which minimizes this expression is the root of
It follows that

(1221)

The fact that confirms our earlier conjecture that the electrons partiallyshield the nuclear charge from one another. Our new estimatefor the ground-state energy of helium is
This is clearly an improvement on our previous estimate (1209) [recall that thecorrect result is eV].

Obviously, we could get even closer to the correct value of thehelium ground-state energy by using amore complicated trial wavefunction with more adjustable parameters.

Note, finally, that since the two electrons in a helium atom are indistinguishable fermions, the overall wavefunction must be anti-symmetric with respect to exchange of particles (see Sect. 6).Now, the overall wavefunction is the product of the spatial wavefunctionand the spinor representing the spin-state. Our spatial wavefunction (1210) is obviously symmetric with respect to exchange ofparticles. This means that the spinor must be anti-symmetric. It is clear, from Sect. 11.4, that if the spin-state ofan system consisting of two spin one-half particles (i.e., two electrons)is anti-symmetric with respect to interchange of particles then the system isin the so-called singlet state with overall spin zero. Hence,the ground-state of helium has overall electron spin zero.

Next:Hydrogen Molecule Ion Up:Variational Methods Previous:Variational PrincipleRichard Fitzpatrick2010-07-20

Learning Objectives

By the end of this section, you will be able to:

• Describe the structure of atoms and the components of nuclei
• Explain the behavior of electrons within atoms and how electrons interact with light to move among energy levels

The idea that matter is composed of tiny particles called atoms is at least 25 centuries old. It took until the twentieth century, however, for scientists to invent instruments that permitted them to probe inside an atom and find that it is not, as had been thought, hard and indivisible. Instead, the atom is a complex structure composed of still smaller particles.

Probing the Atom

The first of these smaller particles was discovered by British physicist James (J. J.) Thomson in 1897. Named the electron, this particle is negatively charged. (It is the flow of these particles that produces currents of electricity, whether in lightning bolts or in the wires leading to your lamp.) Because an atom in its normal state is electrically neutral, each electron in an atom must be balanced by the same amount of positive charge.

The next step was to determine where in the atom the positive and negative charges are located. In 1911, British physicist Ernest Rutherford devised an experiment that provided part of the answer to this question. He bombarded an extremely thin piece of gold foil, only about 400 atoms thick, with a beam of alpha particles (Figure 1). Alpha particles (α particles) are helium atoms that have lost their electrons and thus are positively charged. Most of these particles passed though the gold foil just as if it and the atoms in it were nearly empty space. About 1 in 8000 of the alpha particles, however, completely reversed direction and bounced backward from the foil. Rutherford wrote, “It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.”

Figure 1. Rutherford’s Experiment: (a) When Rutherford allowed α particles from a radioactive source to strike a target of gold foil, he found that, although most of them went straight through, some rebounded back in the direction from which they came. (b) From this experiment, he concluded that the atom must be constructed like a miniature solar system, with the positive charge concentrated in the nucleus and the negative charge orbiting in the large volume around the nucleus. Note that this drawing is not to scale; the electron orbits are much larger relative to the size of the nucleus.

The only way to account for the particles that reversed direction when they hit the gold foil was to assume that nearly all of the mass, as well as all of the positive charge in each individual gold atom, is concentrated in a tiny center or nucleus. When a positively charged alpha particle strikes a nucleus, it reverses direction, much as a cue ball reverses direction when it strikes another billiard ball. Rutherford’s model placed the other type of charge—the negative electrons—in orbit around this nucleus.

Rutherford’s model required that the electrons be in motion. Positive and negative charges attract each other, so stationary electrons would fall into the positive nucleus. Also, because both the electrons and the nucleus are extremely small, most of the atom is empty, which is why nearly all of Rutherford’s particles were able to pass right through the gold foil without colliding with anything. Rutherford’s model was a very successful explanation of the experiments he conducted, although eventually scientists would discover that even the nucleus itself has structure.

The Atomic Nucleus

The simplest possible atom (and the most common one in the Sun and stars) is hydrogen. The nucleus of ordinary hydrogen contains a single proton. Moving around this proton is a single electron. The mass of an electron is nearly 2000 times smaller than the mass of a proton; the electron carries an amount of charge exactly equal to that of the proton but opposite in sign (Figure 2). Opposite charges attract each other, so it is an electromagnetic force that holds the proton and electron together, just as gravity is the force that keeps planets in orbit around the Sun.

Figure 2 is a schematic diagram of a hydrogen atom in its lowest energy state, also called the ground state. The proton and electron have equal but opposite charges, which exert an electromagnetic force that binds the hydrogen atom together. In the illustration, the size of the particles is exaggerated so that you can see them; they are not to scale. They are also shown much closer than they would actually be as it would take more than an entire page to show their actual distance to scale.

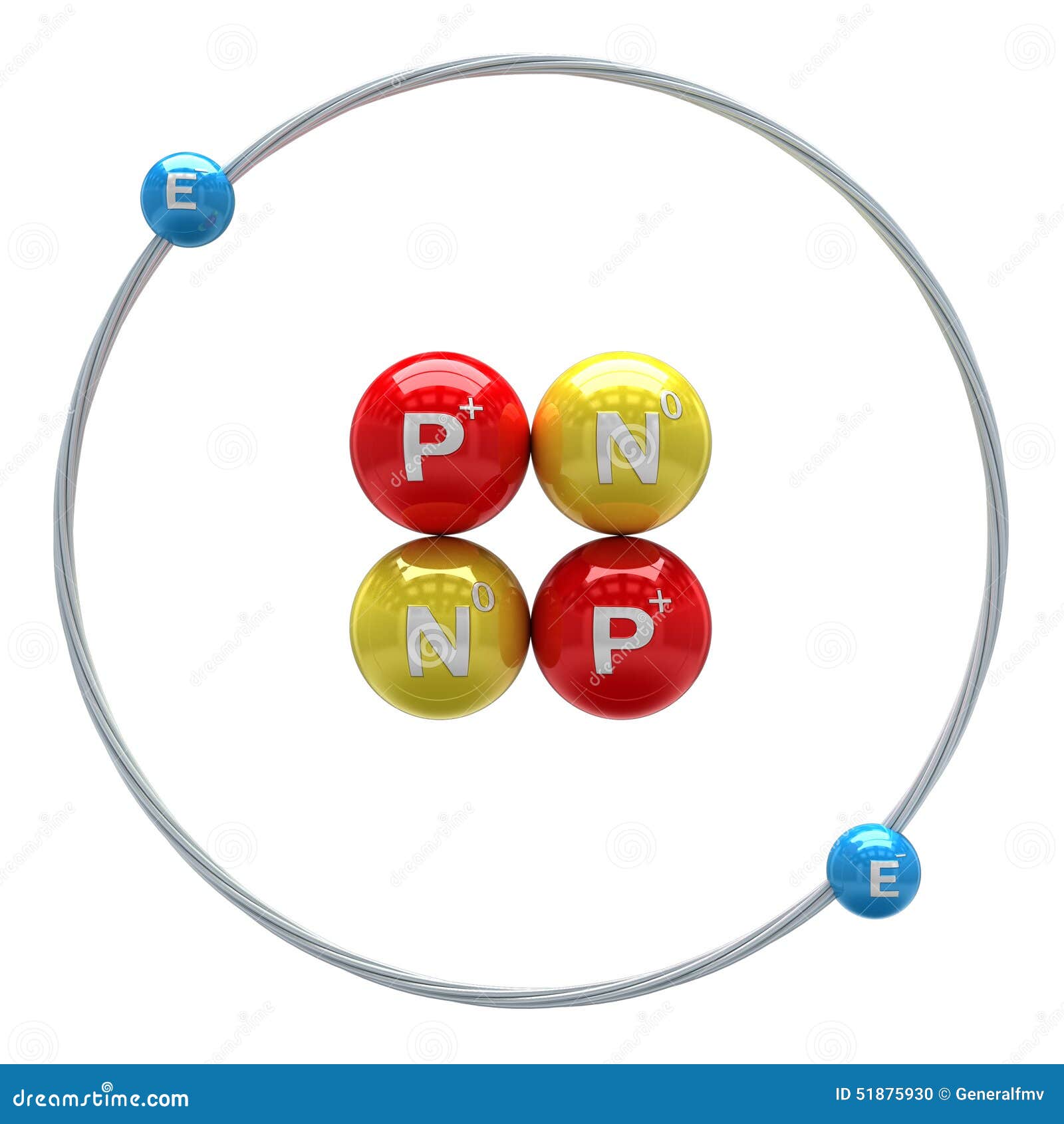
There are many other types of atoms in nature. Helium, for example, is the second-most abundant element in the Sun. Helium has two protons in its nucleus instead of the single proton that characterizes hydrogen. In addition, the helium nucleus contains two neutrons, particles with a mass comparable to that of the proton but with no electric charge. Moving around this nucleus are two electrons, so the total net charge of the helium atom is also zero (Figure 3).

Figure 3: Helium Atom

Figure three is a schematic diagram of a helium atom in its lowest energy state. Two protons are present in the nucleus of all helium atoms. In the most common variety of helium, the nucleus also contains two neutrons, which have nearly the same mass as the proton but carry no charge. Two electrons orbit the nucleus.

From this description of hydrogen and helium, perhaps you have guessed the pattern for building up all the elements (different types of atoms) that we find in the universe. The type of element is determined by the number of protons in the nucleus of the atom. For example, any atom with six protons is the element carbon, with eight protons is oxygen, with 26 is iron, and with 92 is uranium. On Earth, a typical atom has the same number of electrons as protons, and these electrons follow complex orbital patterns around the nucleus. Deep inside stars, however, it is so hot that the electrons get loose from the nucleus and (as we shall see) lead separate yet productive lives.

The ratio of neutrons to protons increases as the number of protons increases, but each element is unique. The number of neutrons is not necessarily the same for all atoms of a given element. For example, most hydrogen atoms contain no neutrons at all. There are, however, hydrogen atoms that contain one proton and one neutron, and others that contain one proton and two neutrons. The various types of hydrogen nuclei with different numbers of neutrons are called isotopes of hydrogen (Figure 4) and all other elements have isotopes as well. You can think of isotopes as siblings in the same element “family”—closely related but with different characteristics and behaviors.

Figure 4: Isotopes of Hydrogen. A single proton in the nucleus defines the atom to be hydrogen, but there may be zero, one, or two neutrons. The most common isotope of hydrogen is the one with only a single proton and no neutrons.

He Atom Model

In this interactive, you can explore the structure of atoms as you add protons, neutrons, or electrons to a model and the name of the element you have created will appear. You can also see the net charge, the mass number, whether it is stable or unstable, and whether it is an ion or a neutral atom.

The Bohr Atom

Rutherford’s model for atoms has one serious problem. Maxwell’s theory of electromagnetic radiation says that when electrons change either speed or the direction of motion, they must emit energy. Orbiting electrons constantly change their direction of motion, so they should emit a constant stream of energy. Applying Maxwell’s theory to Rutherford’s model, all electrons should spiral into the nucleus of the atom as they lose energy, and this collapse should happen very quickly—in about 10^–16 seconds.

It was Danish physicist Niels Bohr (1885–1962) who solved the mystery of how electrons remain in orbit. He was trying to develop a model of the atom that would also explain certain regularities observed in the spectrum of hydrogen. He suggested that the spectrum of hydrogen can be understood if we assume that orbits of only certain sizes are possible for the electron. Bohr further assumed that as long as the electron moves in only one of these allowed orbits, it radiates no energy: its energy would change only if it moved from one orbit to another.

This suggestion, in the words of science historian Abraham Pais, was “one of the most audacious hypotheses ever introduced in physics.” If something equivalent were at work in the everyday world, you might find that, as you went for a walk after astronomy class, nature permitted you to walk two steps per minute, five steps per minute, and 12 steps per minute, but no speeds in between. No matter how you tried to move your legs, only certain walking speeds would be permitted. To make things more bizarre, it would take no effort to walk at any one of the allowed speeds, but it would be difficult to change from one speed to another. Luckily, no such rules apply at the level of human behavior. But at the microscopic level of the atom, experiment after experiment has confirmed the validity of Bohr’s strange idea. Bohr’s suggestions became one of the foundations of the new (and much more sophisticated) model of the subatomic world called quantum mechanics.

In Bohr’s model, if the electron moves from one orbit to another closer to the atomic nucleus, it must give up some energy in the form of electromagnetic radiation. If the electron goes from an inner orbit to one farther from the nucleus, however, it requires some additional energy. One way to obtain the necessary energy is to absorb electromagnetic radiation that may be streaming past the atom from an outside source.

A key feature of Bohr’s model is that each of the permitted electron orbits around a given atom has a certain energy value; we therefore can think of each orbit as an energy level. To move from one orbit to another (which will have its own specific energy value) requires a change in the electron’s energy—a change determined by the difference between the two energy values. If the electron goes to a lower level, the energy difference will be given off; if the electron goes to a higher level, the energy difference must be obtained from somewhere else. Each jump (or transition) to a different level has a fixed and definite energy change associated with it.

A crude analogy for this situation might be life in a tower of luxury apartments where the rent is determined by the quality of the view. Such a building has certain, definite numbered levels or floors on which apartments are located. No one can live on floor 5.37 or 22.5. In addition, the rent gets higher as you go up to higher floors. If you want to exchange an apartment on the twentieth floor for one on the second floor, you will not owe as much rent. However, if you want to move from the third floor to the twenty-fifth floor, your rent will increase. In an atom, too, the “cheapest” place for an electron to live is the lowest possible level, and energy is required to move to a higher level.

Here we have one of the situations where it is easier to think of electromagnetic radiation as particles (photons) rather than as waves. As electrons move from one level to another, they give off or absorb little packets of energy. When an electron moves to a higher level, it absorbs a photon of just the right energy (provided one is available). When it moves to a lower level, it emits a photon with the exact amount of energy it no longer needs in its “lower-cost living situation.”

The photon and wave perspectives must be equivalent: light is light, no matter how we look at it. Thus, each photon carries a certain amount of energy that is proportional to the frequency (f) of the wave it represents. The value of its energy (E) is given by the formula

where the constant of proportionality, h, is called Planck’s constant.

Figure 5. Niels Bohr (1885–1962) and Max Planck (1858–1947): (a) Bohr, shown at his desk in this 1935 photograph, and (b) Planck helped us understand the energy behavior of photons.

The constant is named for Max Planck, the German physicist who was one of the originators of the quantum theory (Figure 5). If metric units are used (that is, if energy is measured in joules and frequency in hertz), then Planck’s constant has the value h = 6.626 × 10^–34 joule-seconds (J-s). Higher-energy photons correspond to higher-frequency waves (which have a shorter wavelength); lower-energy photons are waves of lower frequency.

To take a specific example, consider a calcium atom inside the Sun’s atmosphere in which an electron jumps from a lower level to a higher level. To do this, it needs about 5 × 10^–19 joules of energy, which it can conveniently obtain by absorbing a passing photon of that energy coming from deeper inside the Sun. This photon is equivalent to a wave of light whose frequency is about 7.5 × 10¹⁴ hertz and whose wavelength is about 3.9 × 10^–7 meters (393 nanometers), in the deep violet part of the visible light spectrum. Although it may seem strange at first to switch from picturing light as a photon (or energy packet) to picturing it as a wave, such switching has become second nature to astronomers and can be a handy tool for doing calculations about spectra.

the energy of a pHOton

Now that we know how to calculate the wavelength and frequency of a photon, we can use this information, along with Planck’s constant, to determine how much energy each photon carries. How much energy does a red photon of wavelength 630 nm have?

Show AnswerFirst, as we learned earlier, we can find the frequency of the photon:

[latex]f=frac{c}{lambda}=frac{3times {10}^{8}text{m/s}}{630times {10}^{text{-9}}text{m}}=4.8times {10}^{14}text{Hz}[/latex]

The Atomic Mass Of An Element Is

Next, we can use Planck’s constant to determine the energy (remember that a Hz is the same as 1/s):

[latex]E=hf=left(6.626times {10}^{text{-34}}text{J-s}right)left(4.8times {10}^{14}text{(1/s)}right)=3.2times {10}^{text{-19}}text{J}[/latex]

Check Your Learning

What is the energy of a yellow photon with a frequency of 5.5 × 10¹⁴ Hz?

Show Answer

The Atom Superhero

He Atomic

Key Concepts and Summary

Atoms consist of a nucleus containing one or more positively charged protons. All atoms except hydrogen can also contain one or more neutrons in the nucleus. Negatively charged electrons orbit the nucleus. The number of protons defines an element (hydrogen has one proton, helium has two, and so on) of the atom. Nuclei with the same number of protons but different numbers of neutrons are different isotopes of the same element. In the Bohr model of the atom, electrons on permitted orbits (or energy levels) don’t give off any electromagnetic radiation. But when electrons go from lower levels to higher ones, they must absorb a photon of just the right energy, and when they go from higher levels to lower ones, they give off a photon of just the right energy. The energy of a photon is connected to the frequency of the electromagnetic wave it represents by Planck’s formula, E = hf.

Glossary

energy level: a particular level, or amount, of energy possessed by an atom or ion above the energy it possesses in its least energetic state; also used to refer to the states of energy an electron can have in an atom

Helium Atom Model

isotope: any of two or more forms of the same element whose atoms have the same number of protons but different numbers of neutrons

The Atomic Number Of An Atom Is Equal To The Number Of

nucleus (of an atom): the massive part of an atom, composed mostly of protons and neutrons, and about which the electrons revolve